多支座模拟
写在前面：持续更新……
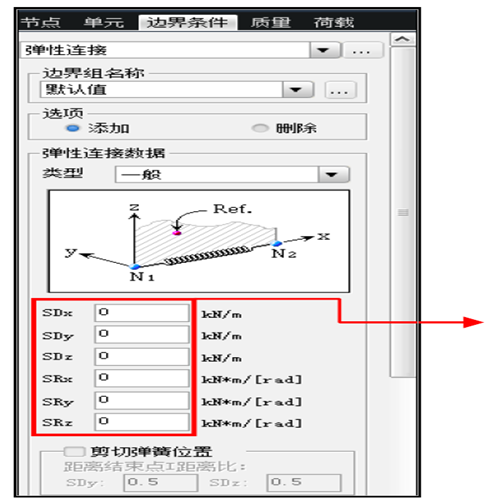
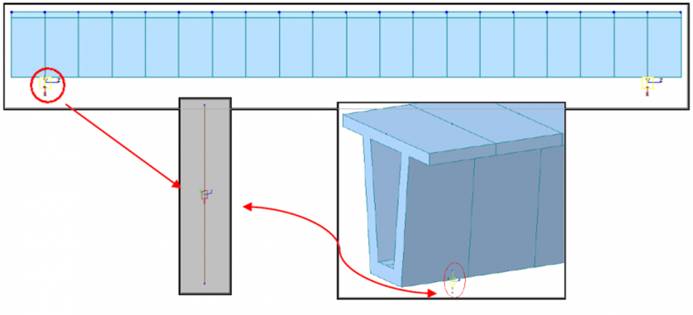
使用“边界条件”→“弹性连接”，模拟支座的 6 个刚度。（如图 1.3、1.4 所示）
以材料力学角度理解：
沿单元局部坐标系 x 轴方向刚度：SDx=EA/L
沿单元局部坐标系 y、z 轴方向刚度：SDy=SDz=GA/L
绕单元局部坐标系 x 轴方向转动刚度：SRx=GIp/L
绕单元局部坐标系 y、z 轴方向转动刚度: SRy=EIy/L、SRz=EIz/L
式中：
E-弹性模量；
G-切变模量；
A-面积；
L-支座高度（厚度）；
Iy、Iz-截面抗弯惯性矩；
Ip-截面抗扭惯性矩。
注：由于在这里输入的各向刚度的单位是线刚度，所以在模拟支座顶、底两个节点的间距时，其间距值可以是实际的支座高度，也可以是为了模型查看方便，设置一个稍大些的值，都不影响分析结果。
4、结合规范（JT/T 4-2004）和（JTG D62-2004）举例说明支座刚度的计算方法
例：我们分别选取矩形支座和圆形支座来计算（实际设计时，支座的选取要根据支反力及 D62 规范来确定）
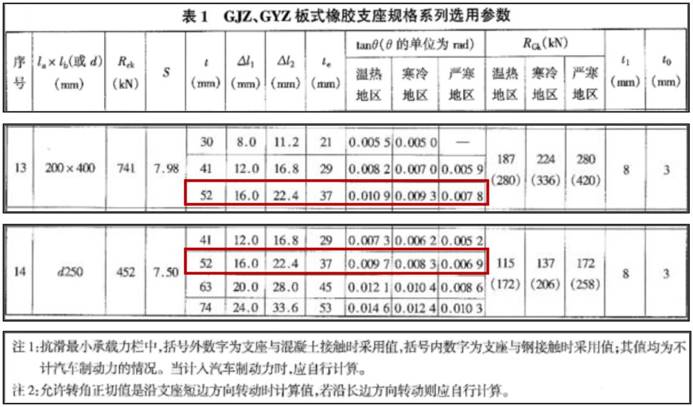
图1.5 板式橡胶支座规格表
① SDx 的计算（即支座的抗压刚度计算）
矩形支座：La×Lb-200×400/52：S=7.98
（注：S 在支座选用表中可直接查到，在此主要是说明计算过程，参见 D62，8.4.1）
支座剪变模量Ge的计算
本例按常温选取，Ge=1MPa（参见 D62，8.4.1）
（注：Ge 选取的值是根据试验得到，同时，试验规定 Ge 的测定是在平均压应力σc =10MPa作用下得到的，也就是说是在承压状态下得到的剪变模量，也就支座不存在刚度计算时，是否在承压状态下计算的刚度这个问题了。
支座抗压弹性模量Ee计算
圆形支座：Ee = 5.4Ge S2 = 5.4 × 1 × 7.52 = 303.75MPa
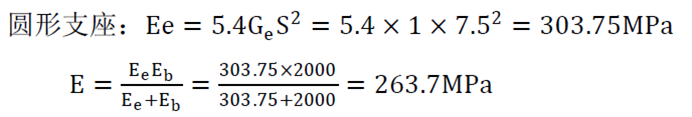
② SDy、SDz 的计算（即支座的剪切刚度计算）
材料力学的角度计算公式：SDy=SDz=GA/L，结合规范后的计算方式如下：
i.G 的计算（G=Ge=1MPa 参见 D62，8.4.1）
ii.A 的计算（A=kAe，计算见前页 Ae 计算，圆形 k=0.9,矩形 k=5/6，参见帮助文档-截面-剪切面积部分）
iii.L 的计算（L=te，计算过程略，参见 SDx 中的 te 计算）
综上，midas Civil 中弹性连接沿局部坐标 y、z 轴方向刚度 SDy=SDz
③ SRx 的计算（即支座的抗扭刚度计算）
材料力学的角度计算公式：SRx=GIp/L，结合规范后的计算方式如下：
i. Ip 的计算（支座截面的抗扭刚度）
抗扭刚度 Ip 是抵抗扭矩的刚度。它不同于为了计算扭矩作用下的截面剪应力所使用的极惯性矩。但是，当截面形状是圆形或厚板圆环时，其抗扭刚度与极惯性矩相同。
在 midas Civil 的帮助文件中，给出了常见截面 Ip 的计算公式，如图 1.7 所以：
普通板式橡胶支座介绍
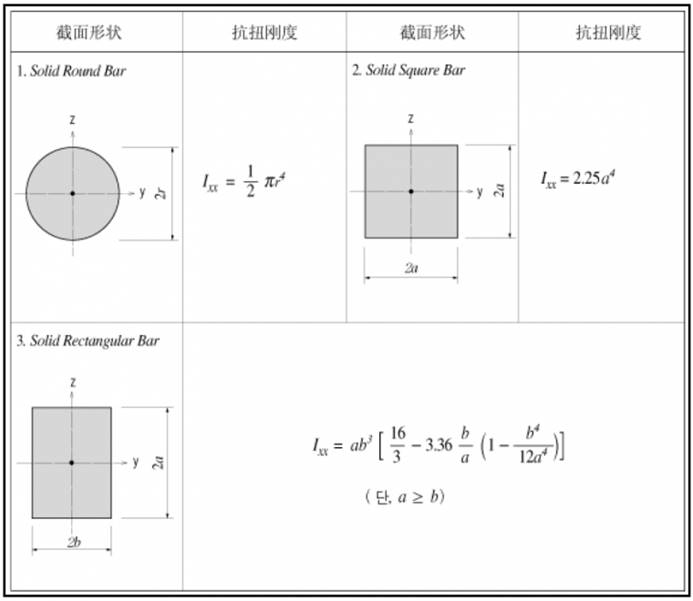
（注：此处所列的计算公式与材料力学中扭转部分的扭转刚度计算一致，只是表达形式不同而已，对于更复杂的截面可以借助Civil截面特征中的特性值计算功能直接求得）
④ SRy、SRz的计算（即支座的抗弯刚度计算）
材料力学的角度计算公式：SRy=EIy/L、SRz=EIz/L，结合规范后的计算方式如下：
· E的计算（同上）
· L的计算（同上）
· Iy和Iz的计算
（注：根据材力中的转动刚度公式可推导出SRx、SRy、SRz的单位为：N·mm/rad）
⑤ 橡胶支座用弹性连接模拟刚度计算完成
将表1.1中的刚度数据填到程序中的“弹性连接”对话框中。
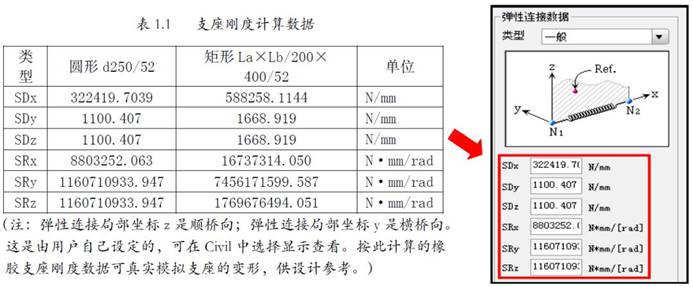
图1.8 输入弹性连接的刚度
到此我们已经可以计算出橡胶支座的具体刚度数据，那么在具体使用时，需要注意以下几点。
① 我们在计算SDx时，考虑到D62-8.4.2-8条文参考了美国、欧洲规范，在计算竖向压缩变形的时候考虑橡胶弹性体体积模量（Eb），取值2000MPa。所以，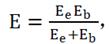
，具体的公式推导就是将D62-8.4.2-8公式进行变形得出等效E值的计算公式。
② 支座剪变模量Ge计算的时候，按D62-8.4.1选取为1.0Mpa，在进行抗震计算的时候，应该按08细则6.3.7-1式选取为1.2MPa。
③ 支座有效承压面积按有效承压加劲钢板面积Ae取值，计算不同形状支座有效剪切面积的时候，要考虑支座形状的影响，圆形为0.9，矩形为5/6，具体可参见Civil的帮助手册“截面”部分。
④ 本资料中给出的SDy、SDz水平剪切刚度的计算方法，只适用于在纯剪切模式下，小变形范围内的主梁受力分析时，所采用的剪切刚度计算公式。如果要进行抗震分析，我们还需考虑支座在受到地震水平力作用下会发生较大的变形，此时的支座剪切刚度应该按压弯模式下计算，具体的计算方法会在后续的桥梁荟期刊中给出，用户也可以参考范立础编著的《桥梁减隔震设计》这本书，自行学习。
⑤ 虽然我们按上述方法计算出3个平动（SDx、SDy、SDz）和3个转动（SRx、SRy、SRz）自由度的支座刚度，但是，这些刚度数据其实是支座本身的刚度，具体到与实际工程中的设置，主梁一般是放置在橡胶支座上的，主梁与支座顶面没有固结，也就是说，3个转动刚度和2个平动刚度（SDy、SDz）是否能完全发挥作用，还是要考虑主梁与支座表面的摩擦力的大小。
⑥ 一般的处理方式，我们只需输入3个平动刚度即可正确的得到我们想要到主梁内力结果，因为，实际中转动刚度是支座本身的刚度，并不意味着给主梁提供了相应的刚度。
⑦ 我们计算的转动刚度SRx、SRy、SRz也是有用的，因为是近似真实的支座刚度数据，分析后，我们可以查看支座单元的分析结果，核对支座的变形及相应受力情况。